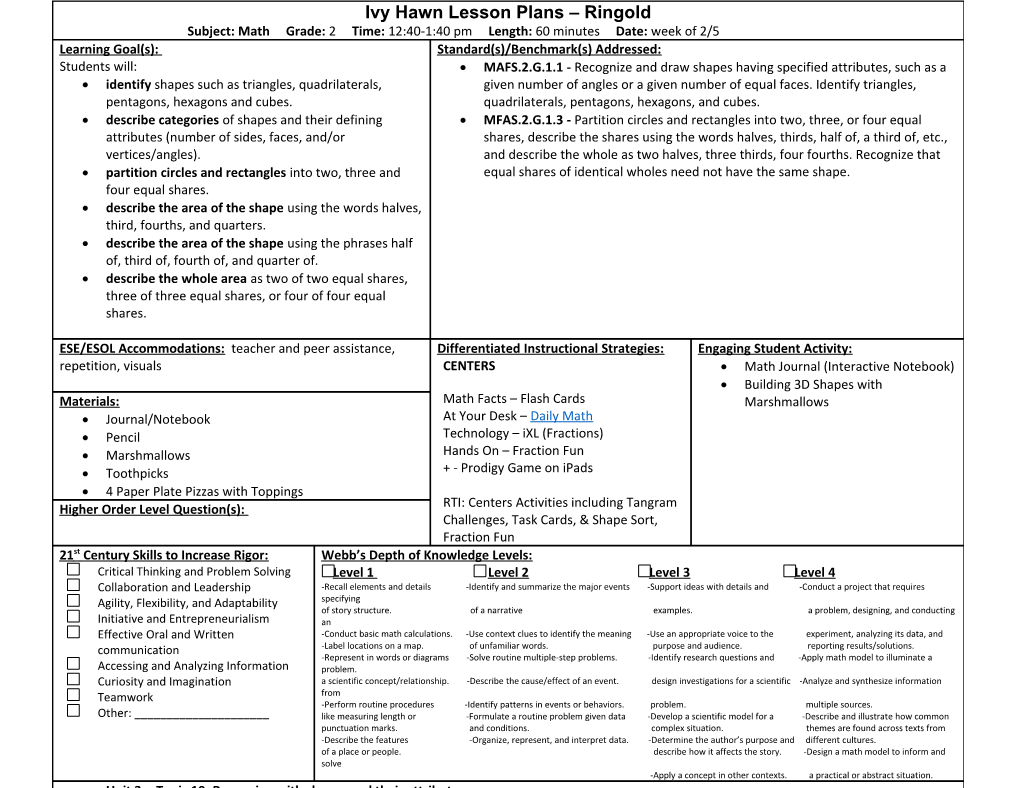
Ivy Hawn Lesson Plans – Ringold
Subject: Math Grade: 2 Time: 12:40-1:40 pm Length: 60 minutes Date: week of 2/5
Learning Goal(s):
Students will:
· identify shapes such as triangles, quadrilaterals, pentagons, hexagons and cubes.
· describe categories of shapes and their defining attributes (number of sides, faces, and/or vertices/angles).
· partition circles and rectangles into two, three and four equal shares.
· describe the area of the shape using the words halves, third, fourths, and quarters.
· describe the area of the shape using the phrases half of, third of, fourth of, and quarter of.
· describe the whole area as two of two equal shares, three of three equal shares, or four of four equal shares. / Standard(s)/Benchmark(s) Addressed:
· MAFS.2.G.1.1 - Recognize and draw shapes having specified attributes, such as a given number of angles or a given number of equal faces. Identify triangles, quadrilaterals, pentagons, hexagons, and cubes.
· MFAS.2.G.1.3 - Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Recognize that equal shares of identical wholes need not have the same shape.
ESE/ESOL Accommodations: teacher and peer assistance, repetition, visuals / Differentiated Instructional Strategies:
CENTERS
Math Facts – Flash Cards
At Your Desk – Daily Math
Technology – iXL (Fractions)
Hands On – Fraction Fun
+ - Prodigy Game on iPads
RTI: Centers Activities including Tangram Challenges, Task Cards, & Shape Sort, Fraction Fun / Engaging Student Activity:
· Math Journal (Interactive Notebook)
· Building 3D Shapes with Marshmallows
Materials:
· Journal/Notebook
· Pencil
· Marshmallows
· Toothpicks
· 4 Paper Plate Pizzas with Toppings
Higher Order Level Question(s):
21st Century Skills to Increase Rigor:
Critical Thinking and Problem Solving
Collaboration and Leadership
Agility, Flexibility, and Adaptability
Initiative and Entrepreneurialism
Effective Oral and Written communication
Accessing and Analyzing Information
Curiosity and Imagination
Teamwork
Other: ______
/ Webb’s Depth of Knowledge Levels:
Level 1 Level 2 Level 3 Level 4
-Recall elements and details -Identify and summarize the major events -Support ideas with details and -Conduct a project that requires specifying
of story structure. of a narrative examples. a problem, designing, and conducting an
-Conduct basic math calculations. -Use context clues to identify the meaning -Use an appropriate voice to the experiment, analyzing its data, and
-Label locations on a map. of unfamiliar words. purpose and audience. reporting results/solutions.
-Represent in words or diagrams -Solve routine multiple-step problems. -Identify research questions and -Apply math model to illuminate a problem.
a scientific concept/relationship. -Describe the cause/effect of an event. design investigations for a scientific -Analyze and synthesize information from
-Perform routine procedures -Identify patterns in events or behaviors. problem. multiple sources.
like measuring length or -Formulate a routine problem given data -Develop a scientific model for a -Describe and illustrate how common
punctuation marks. and conditions. complex situation. themes are found across texts from
-Describe the features -Organize, represent, and interpret data. -Determine the author’s purpose and different cultures.
of a place or people. describe how it affects the story. -Design a math model to inform and solve
-Apply a concept in other contexts. a practical or abstract situation.
Unit 3: Topic 10: Reasoning with shapes and their attributes
Lesson Activity/Experiences:
· Monday:
o Open/Engage: Cubie the Ice Cube by Jack Hartman Show video clip to engage students. Have them share where they have seen or used cubes.
o Whole Group: Arrange desks so that students are sitting in groups of four. Distribute a bag of toothpicks and marshmallows for constructing a cube to each group, as well as 1 piece of 8½″ × 11″ white paper per student.
o Part 1: Constructing a Cube
§ Watch as I use four toothpicks to build a square. (Build a square as shown at right.) It’s your turn. Use four toothpicks and some sticky tack to build a square! (Allow time to work.) Using words we have learned in the past week, describe your square to your partner. (It has four straight sides that are the same length. It has four square corners. It can be called lots of different names: a polygon, a quadrilateral, a square. ) A square can also be used to build a solid shape that has equal edges. Here is a cube. (Hold up a cube.) What shape are the faces of this cube? (Squares! )
§ I want to build a cube with toothpicks. How many would I need? (Give students time to consider) Let’s count the edges to find out. (Count the edges, marking each one as you go.) First, we’ll count the edges on the bottom: 1 edge, 2 edges, 3 edges, 4 edges. Now, the edges around the middle: 5 edges, 6 edges, 7 edges, 8 edges. Now, those around the top: 9 edges, 10 edges, 11 edges, 12 edges. How many edges does a cube have? (Twelve edges!)
§ Can we use this square that we already built to construct our cube? (Yes!) Talk to your partner. How many more toothpicks do we need to build the cube? (S: 12 – 4 = 8. Eight more toothpicks. ) Get eight more toothpicks and some more sticky tack, and see if you can use your square to make a cube that looks like my cube.
o Small Group: Students will work with their small groups to construct a cube using toothpicks. Student partners may need to help each other stabilize their cubes as they are building.
o Centers
· Tuesday:
o Open/Engage: Read aloud Give Me Half by Stuart J Murphy. Say "Think about a time you have had to share something with a friend, a brother, or a sister. Turn and talk to your neighbor about the time you had to share something" After a minute, say "I heard ______discussing that one time when sharing a ______he/she got the smaller piece. If I shared this cookie with (student) like this (break the cookie in very unequal pieces) would that be fair?" Discuss with the students. Lead the students to determine that the whole cookie needs to be cut in half so each person gets the same amount. Introduce the students to the vocabulary words whole, half, and half of.
o Whole Group: Display the pizza model (1 of 3 paper plates with the pizza glued onto it) and explain that the pizza represents one whole. Ask the students if their families have ever ordered pizzas that were half pepperoni and half cheese.
§ Invite a student to demonstrate how to divide the one whole pizza into halves. Cut the pizza in half. Discuss the fact that the halves are equal shares and that the two halves together equal one whole.
§ Once the pizza is divided into halves, invite the student to make one-half of the pizza pepperoni and one-half cheese using the toppings you have colored and cut out. Emphasize that there are two equal shares.
§ Take another paper plate, fold it in half and then half again. Ask the students how many equal shares the whole pizza has been divided into. [four] Does anyone know what each part would be called. (fourths)
§ Invite a student to come to the front of the class and make a pizza that is one equal share pepperoni, one equal share cheese, one equal share mushroom and one equal share plain.
§ Cut the third paper plate into thirds. Ask the students what they think the number is that describes each equal share.
§ Have a student place 3 ingredients on the pizza in equal shares and ask the rest of the class to tell what word represents the equal shares.
§ Call out equal share names and invite students to indicate to which plate parts you’re referring. Then do the reverse by showing students a fractional part of the plate and asking them which equal share it represents.
o Small Group: Inform them that they are going to work together in pairs with one student being a pizza chef and the other student being the waiter.
§ Distribute scissors, glue sticks, Pizza Order Forms and Toppings, Pizza – Small Group to each pair. Have students cut them apart.
§ Ask the waiters to raise their hands. Tell them to choose an order from those they cut apart. After they fill in their names and the names of their partners, have them present the orders to the chefs.
§ The chefs should then mark the pizzas into fractional units and glue the ingredients as directed. When the pizzas are completed, direct the waiters to check the orders.
§ Have students set the pizzas and orders aside, switch roles, and continue with other orders until all six pizzas have been made and checked.
o Centers
· Wednesday:
o Whole Group: Give directions on how to cut out, glue, and paste the interactive NB page on fractions (sort).
o Small Group: Students will work independently and/or with a partner to sort and paste the fractions under the correct flap.
o Centers
· Thursday –
o Open/Engage: Read aloud Eating Fractions, by Bruce MacMillan.
o Whole Group: T: (Call on a volunteer, and give him one half of a circle from the labeled fraction parts template.) Look at the part ____ is holding. Does she/he have a whole circle? (No. ) What does he need to complete the circle? (Another half! ) Watch as I complete the whole. (Hold the other half of the circle next to the student’s part.) 1 half and 1 half make 1 whole; 2 halves make a whole! Say it with me. (1 half and 1 half make a whole. 2 halves make a whole. )
o (Call two volunteers, and give them each one-third of a rectangle from the labeled fraction parts template.) Look at the parts of a rectangle ____ and ____ are holding. They each have 1 third of a rectangle. How many thirds do you see altogether? (2 thirds.) What do they need to complete the whole rectangle? (1 more third.) Yes. Watch as I complete the whole. (Hold 1 third of the rectangle next to the others.) 1 third and 1 third and 1 third make a whole; 3 thirds make a whole! Say it with me. ( 1 third and 1 third and 1 third make a whole; 3 thirds make a whole. )
o (Call three volunteers, and give them each 1 fourth of the square template.) Look at the parts of a square that _____, ______, and ______are holding. They each have 1 fourth of a square. What do they need to complete the whole square? (1 more fourth.) Let’s complete the whole. (Finish the shape to correctly form a square.) Good thinking, everyone. This one was tricky. 1 fourth and 1 fourth and 1 fourth and 1 fourth make 1 whole; 4 fourths make 1 whole. Say it with me. (1 fourth and 1 fourth and 1 fourth and 1 fourth make 1 whole; 4 fourths make 1 whole.)
o (From the previously cut labeled fraction parts templates, distribute one piece of a whole circle (halves, thirds, or fourths) to each student.) Each of you has a piece of a whole circle. When I say, “Find your whole,” walk around the room to complete your whole. Ready? Find your whole! Do all of our groups have the same number of people? (No! ) Which group has the most people? Which group has the fewest number of people? ( The fourths have the most people because it takes 4 fourths to make the whole circle. The halves have the fewest number of people because it only takes 2 halves to make a whole.) Which group has the biggest pieces? Which group has the smallest pieces? (The halves are the biggest. The fourths are the smallest.) So what can we say about thirds compared to halves and fourths? (Thirds are bigger than fourths but smaller than halves! A shape can have more thirds than halves. )
o Centers
· Friday:
o Fractions Formative
o Centers
Reading, Math, 4Th Writing, 5Th Science s3