Supplementary 1: Homogenization of the observeddata from the surface stations
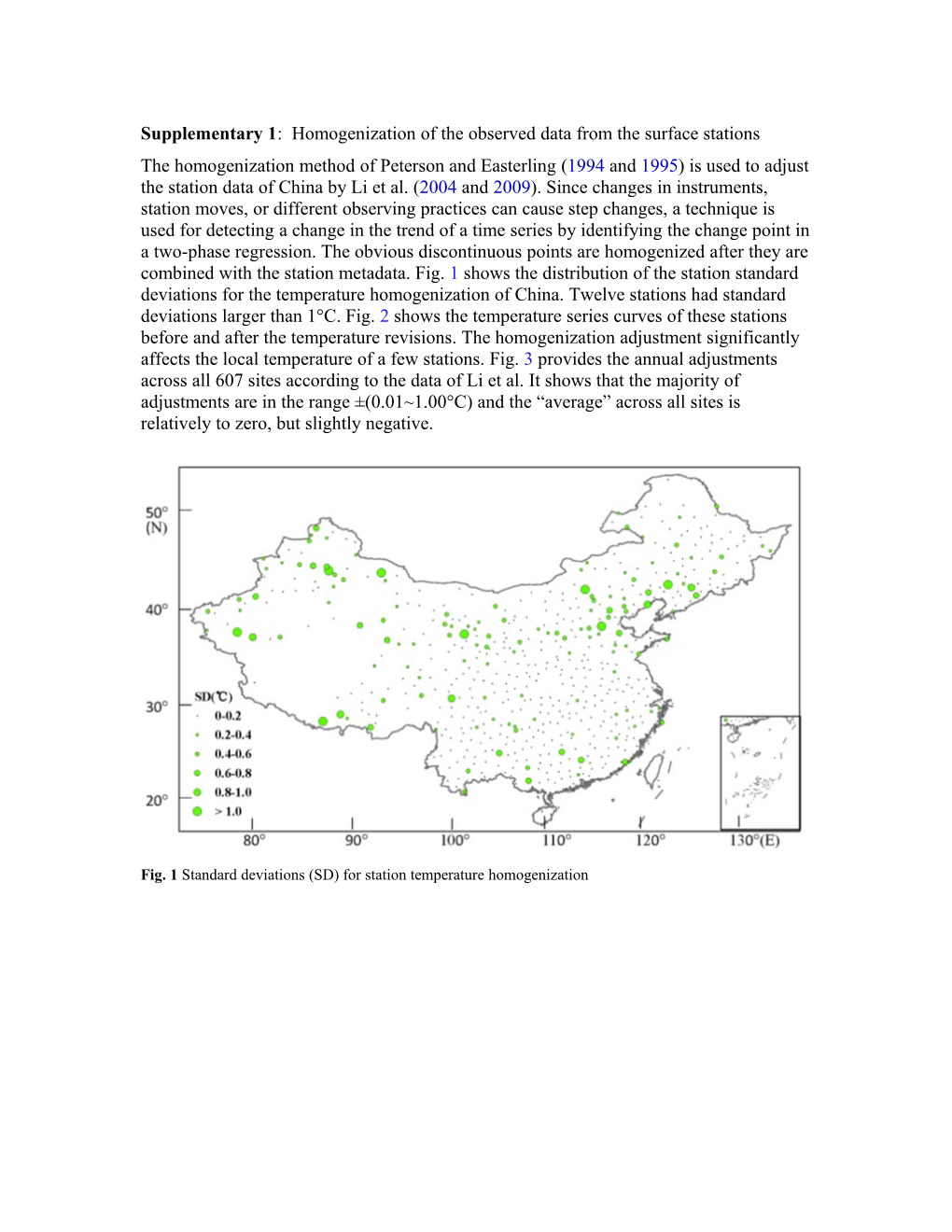
The homogenization method of Peterson and Easterling(1994 and1995) is used to adjust the station data of China by Li et al. (2004 and2009). Since changes in instruments, station moves, or different observing practices can cause step changes, a technique is used for detecting a change in the trend of a time series by identifying the change point in a two-phase regression. The obvious discontinuous points are homogenized after they are combined with the station metadata. Fig. 1 shows the distribution of the station standard deviations for the temperature homogenization of China.Twelve stations had standard deviations larger than 1°C. Fig. 2 shows the temperature series curves of these stations before and after the temperature revisions. The homogenization adjustment significantly affects the local temperature of a few stations.Fig. 3 provides the annual adjustments across all 607 sites according to the data of Li et al. It shows that the majority of adjustments are in the range±(0.01~1.00°C) and the “average” across all sites is relatively to zero, but slightly negative.
Fig. 1Standard deviations (SD)for station temperature homogenization
Fig. 2Temperature series from the stations with standard deviations larger than 1℃. The blue line indicates the pre-adjustment series and the red line indicates the post-adjustment series.
Fig. 3Distribution of annual stationhomogeneity adjustments
Notice thatthe vertical axis corresponds to the relative frequency of each data value, which is written in decimal form. The relative frequencies sum to 1.The histogram is based on adjustments from 607 stations from CMA.
Supplementary 2: Treatment of missing data
The missing values are estimated using linear interpolation of data from the neighboring stations.The reference neighboring stations are selected according to the following criteria: the high correlation of temperature records with a coefficient (r) higherthan 0.8 for the nearest 30 years around the missing year, the similar elevation, and the similar land surface configuration. To evaluate the statistical fidelity of these regressionmodels, the split-sample calibration–verification tests (Mekoand Graybill, 1995) are used. The two most rigorous tests of modelvalidation (the reduction of error (RE) and the coefficientof efficiency (CE))are calculated. The following Table1 shows the sample results for Tianjin station.The closer that the value is to 1, the better the regression model is. Totally, the values of RE and CEare almost positive for all models. Thetest results show the validity of the regression model.
We compare the differences between two mean annual temperature time-series before and after missing data imputation (Fig. 4). In general, the data imputation does not significantly influence the temperature trend, and only minor differences are present over several years. The standard deviation of the annual difference series is 0.012°C. The seasonal analysis shows similar results as the annual mean temperature (not shown).
Table 1 Statistics of calibration and verification test results for the Tianjinstation
Calibration(1954-1973) / Verification
(1974-1983) / Calibration
(1964-1983) / Verification
(1954-1963) / Full calibration
(1954-1983)
r / 0.98 / 0.99 / 0.97 / 0.87 / 0.98
RE / - / 1.00 / - / 0.52 / -
CE / - / 0.92 / - / 0.45 / -
Fig. 4Annual mean temperature anomaly before and after missing data imputation for China
Supplementary 3:Satellite observed land-use data
The land use database is developed by the ChineseAcademy of Sciences (CAS). The original data were derivedfrom satellite remote sensing data provided by the US Landsat TM/ETM images which have a spatial resolution of 30 by 30 meters (Vogelmann et al.2001). These have been aggregated by CAS into 100 by 100 meters picture elements (‘pixels’) (Liu et al.2002 and 2005). We use theperiod selected from 1980 onwards. For each time period more than 500 TM scenes are used to cover the entire country. The CAS data team also spent considerable time to validate the interpretation of the images and land-cover classifications against extensive field surveys (Liu et al.2002). These Landsat-TM/ETM images were geo-referenced and orthorectified, using field-collected ground control points and high-resolution digital elevation models. For each TM/ ETM scene, there are at least 20 evenly distributed sites served as Ground Control Points (GCPs). Visual interpretation and digitization of images at the scale of 1:100,000 were done to generate thematic maps of land cover under technical support from Intergraph MGE (Modular GIS Environment) software. A hierarchical classification system of 25 land-use classes was originally applied to the data and the CAS data team aggregates these further into six classes of land use–cultivated land, forestry area, grassland, water area, residential and industrial land(including urban built-up land, other industrial land, and rural residential land) and unused land. The urban built-up land is comprised of areas of intensive use with much of the land covered by structures. The industrial lands are such as large industrial areas, factories, oil fields, salt works, quarries, transport roads, and airports.
Urban land-use types include urban built-up land and other industrial land uses in large, medium and small cities and towns. Fig. 5 shows urban land use in China for the selected period, with each cell representing a 100 m by 100 m pixel.Fig. 5a presents the recent urban land-use coverage, which is 0.67% of the total area of China. Fig. 5b shows the increase in urban land use since 1980.
Fig. 5Urban land use in China
a. 2005 b. increases since 1980. The processed image of urban landuse is from satelliteobservation. The unit is one pixel with 100m by 100 m.
Supplementary 4:Dividing method of urban and reference stations
To divide the stations into urban or rural types, we extract land data from the area immediately surrounding a givenmeteorological station.Various distances around the weather stations are selected for determining the radius of the area surrounding a station with greatest correlation betweenannual temperature trends (⊿T) and urban land-expansion(⊿U). Buffers to a radius of 50 kmare developed around every station, and we calculate the correlation coefficient(r) between ⊿Tand ⊿U at every 5 km increment (i.e. 1 km,5 km, 10 km,…, 50 km). Fig. 6 presents r values for the various radii around the stations. High values are found at10–20 km; beyond that, correlation decreased gradually. At radii from 10–20 km, r was calculated again at every 1 kmincrement, finding the highest value at radius 11 km, withr = 0.217 (n = 607) statistically significant at the 95% level(r = 0.217t0.05,607 = 0.08). Therefore, we choose urban landusedata within an11 kmcircle (unit distance) surroundingeach station to designate sites as either urban or reference stations.
Fig. 6Correlation of annual temperature trend and urban land-use change at variable distances around sites.
The urban land-use change refers to the increase over the 1980 level. The temperature trend is the temperature increase in corresponding period.
The result indicates that 95% of all stations have experienced significant urban land-use expansion in their surroundings. Therefore, it is difficult to select adequate numbers of reference stations that are free from urbanization effects overall of China. Stations with the least urban landuse are regarded as such reference stations.To be definedas a reference station, the urban area in the unit distance surrounding the station must have been less than 1%; otherwise, the station is designated an urban station. In certain highly urbanized areas (e.g., eastern China), several neighboring grids may have had no reference station. For these regions, a less strict reference-station criterion is applied, in which the urban area can be larger than 1% but less than 10%, and the urban land use over the past several decades is not expanded greatly. Fig. 7 shows the distribution of urban and reference stations. There are 196 reference stations (in blue) and 411 urban stations (in red).
Fig. 7The distribution of meteorological stations in China used for this study covering the period 1951-2010 (Red- urban stations, blue- reference stations(see Sect. 4.2).
Supplementary5:Estimation of uncertainties
Surface temperature errors originate from station error, bias error, imputation error, sampling error, and interpolation error. Because these errors are independent, the total error is the root of the sum of squares of all errors. The errors are estimated according to Brohan et al.’s (2006) calculation method.
(1) Station error
The uncertainty in the reported station temperature originates from the measurement error, homogenization adjustment error, and normal error (it is caused by subtracting the station normal from the observed temperature). For the measurement error (ob), the random errorin a single thermometer reading is about0.2°C(Folland et al. 2001), the monthlyaverage will be based on at least two readings aday throughout the month, giving 60 or morevalues contributing to the monthly mean, and 730 or morevalues contributing to the yearly mean. So the station errorin the yearly average will be at most = 0.007 °C, and this will be uncorrelatedwith the value for any other station orthe value for any other month or year.The homogenization adjustment error (H) results from homogenization adjustments. Inhomogeneities are introduced into the stationtemperature series by changes in the station site, changes in measurementtime, or changes in instrumentation (Brohan et al.2006).So the station data were adjusted to remove these inhomogeneities.But such adjustments are notexact, and the resultingHis estimated according to the error value of 0.4 °C from Brohan et al. (2006) as the homogenization adjustment error of individual station.The total adjustment errors of all stations are calculated based on , where n is the station number.The normal error (N) results from the normalization of the observed temperature. The station temperature in each month duringthe normal period can be considered as thesum of a constant stationnormal value and a random weather value(with standard deviation). The normal error is where N is the number of years for which there is data in the normal period.
(2) Bias error
Bias error has two sources: the effect of urbanization and the exposure of thermometer. We discuss the former effect in more details later in this paper. Regarding the exposure of the thermometer, note that after the 1950s thermometers have been placed in instrument shelters; therefore, this problem no longer exists.
(3) Imputation error
Missing monthly station data imputation via interpolation causes errors. The method used to calculate the imputation error when Station A has missing data and Station B is close to A and is expected to be the most relevant is as follows. First, a regression model is fitted to the monthly temperature data of Stations A and B during a period without missing data. Then, the missing temperature data of Station A are simulated using the predicted values from the model. Finally, the standard error of the regression slope is calculated as the imputation error. This is done for each single month and the annual valuesfor different yearsare the mean of all monthly values at each year.
(4) Sampling error(SE)
SE occurs when the temperature estimate does not represent the true grid value because there are notenough stations within the grid box. We use Jones et al.’s (1997) calculation method to estimate the SE of each grid-box. Then the SE of the region is calculated using the large-scale regional average method applied by Smith et al. (1994) and Jones et al. (1997).
First, we calculated the SE of each grid point,
(1)
where is the temperature mean variance of each station within the grid point, is the average correlation coefficient between stations, and n is the number of stations in the grid point.
For grid points with multiple stations,was calculated using the station data. For grid points with few stations, was calculated using the theory of temperature correlation decay length. This expression is
(2)
whereX is the diagonal length of the grid point, and x0is the correlation decay length. To calculate the correlation decay length, please refer to Briffa et al. (1993).
To avoid the influences of station relocation and station density change, the temperature mean variance of the stations at grid point can be calculated as
(3)
whereis the estimation of grid-point temperature variance during the climate reference period, and n is the average number of stations in the grid point during the climate reference period.
Second, we calculated the SE of the region using the large-scale regional average method. The regional average of SEregion is
(4)
whereis the area-weighted average of the grid-point sampling variance, and Neff is the degrees of freedom. This equation can be expressed as
(5)
(6)
where R is the radius of Earth, and is the average correlation decay length of the region.
(5) Interpolation error
Interpolation error occurs during interpolation because of incomplete data coverage when gridding the station data. There are two types of interpolation errors: (a) when there is no station in the grid and interpolation is performed with regard to the nearest station within a neighboring grid; and (b) when there is no rural station in the grid, but most of the region is agricultural land and interpolation is performed with regard tothe nearest rural station. The method used to calculate the interpolation error is as follows.Assume that stations A, B, C, D, and E exist in certain regions. Now, suppose that the stations B-E do not exist; in this case, the temperature of station A is used to impute the temperatures of stations B-E. We are able to calculate the decay region of the interpolation error for station A. As shown in Fig. 8, the y-axis is the temperature standard deviation between station A (for example) and stations B-E. The x-axis represents the distance between station A and its neighboring stations. The scatterplot suggests that the shorter distances between stations predict smaller temperature standard deviations and also the more accurate value of interpolation. An exponential relationship can be obtained via modeling the relationship of standard deviations and distances amongstations. Now, suppose we need to use the temperature of station A to interpolate that of station F; the interpolation error of station F can be calculated by substituting the distance between stations A and F into the exponential model. Here the 4 examples shown in Fig. 8 are selected randomly.
Fig. 8The temperature Standard Deviations (SD) between annual station anomalies and the distance between 4 selected stations.(The solid line is the exponential model fit)