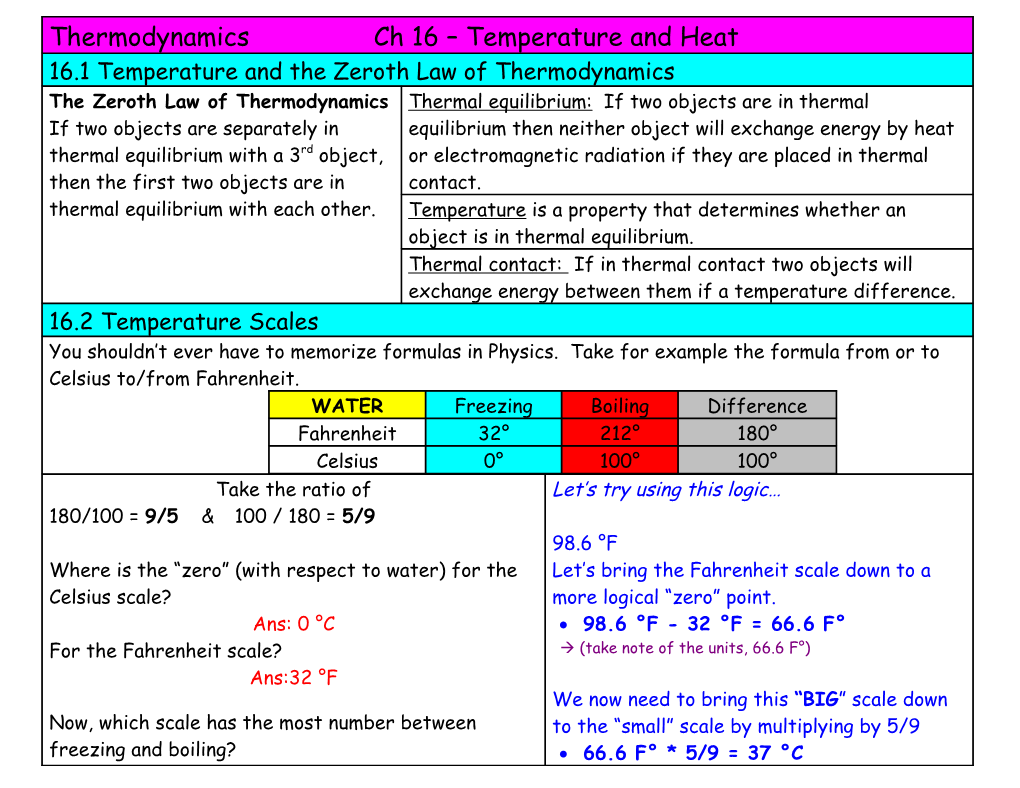
Thermodynamics Ch 16 – Temperature and Heat
16.1 Temperature and the Zeroth Law of Thermodynamics
The Zeroth Law of Thermodynamics
If two objects are separately in thermal equilibrium with a 3rd object, then the first two objects are in thermal equilibrium with each other. / Thermal equilibrium: If two objects are in thermal equilibrium then neither object will exchange energy by heat or electromagnetic radiation if they are placed in thermal contact.
Temperature is a property that determines whether an object is in thermal equilibrium.
Thermal contact: If in thermal contact two objects will exchange energy between them if a temperature difference.
16.2 Temperature Scales
You shouldn’t ever have to memorize formulas in Physics. Take for example the formula from or to Celsius to/from Fahrenheit.
WATER / Freezing / Boiling / Difference
Fahrenheit / 32° / 212° / 180°
Celsius / 0° / 100° / 100°
Take the ratio of
180/100 = 9/5 & 100 / 180 = 5/9
Where is the “zero” (with respect to water) for the Celsius scale?
Ans: 0 °C
For the Fahrenheit scale?
Ans:32 °F
Now, which scale has the most number between freezing and boiling?
Fahrenheit (we’ll call this the “BIG” scale; conversely Celsius is the “small” scale)
So we say the “zero” point for the Fahrenheit scale is 32 °F…
· I think most people will agree this is a weird “zero” point
· How can we bring this “zero” point to zero?
o Ans: Subtract 32 °F
· We also recognize that the Fahrenheit scale is the “BIG” scale…so how can we bring it to a small scale?
o Ans: Multiply by a small ratio, 5/9 / Let’s try using this logic…
98.6 °F
Let’s bring the Fahrenheit scale down to a more logical “zero” point.
· 98.6 °F - 32 °F = 66.6 F°
à (take note of the units, 66.6 F°)
We now need to bring this “BIG” scale down to the “small” scale by multiplying by 5/9
· 66.6 F° * 5/9 = 37 °C
Let’s go in reverse…
37 °C uses the “small” scale
à let’s go to the “BIG” scale
· 37 °C * 9/5 = 66.6 F°
But the “zero” point of the Fahrenheit scale isn’t “zero”…it’s 32 °F
· 66.6 F° + 32 F° = 98.6 °F
The Kelvin scale is the proper scale in most situations (PV = nRT, etc). When in doubt…just use the Kelvin scale. Why?
1 Kelvin = 1 °C and T = TC + 273.15
So if the temps are given in °C then ΔT will be the same
whether in the Kelvin or Celsius scales.
If you notice
T à temperature in the Kelvin scale
TC à temperature in Celsius
TF à temperature in Fahrenheit
The Kelvin scale is an absolute scale which means you
can not go below zero.
At 0 K (do not use the degree sign) all movement (i.e. in an atom) stops. As you can see, we can not achieve the Absolute Zero point, but we can achieve temps very close. / (optional)
Thermometers make use of thermometric properties.
Types of thermometers
· volume expansion (Hg column)
· constant volume gas (Δ gas pressure)
· thermocouples (Voltage differences of two different metals)
· electrical resistance (Platinum wire)
· thermographic (emitted radiation)
Galileo’s Thermometer Demo: TH-E-GT
16.3 Thermal Expansion (of Solids and Liquids)
Let’s pretend we have a 10 cm steel ruler an a 2 meter stick (also steel)
If we heat both of the steel sticks…which will expand more a greater amount?
Most of you will say the long one will expand more and you’ll be RIGHT!
Some may say they will expand the same and you’ll be CORRECT also (almost)!
Explanation:
Since they are both steel, they will expand by the same proportion; but not the same amount…
(We know the longer one will expand by the greater total length since 5% of 2 meters is much greater than 5% of 10 centimeters) / Now let’s pretend we have two 10 cm steel rulers, A and B.
10 cm steel ruler, A, undergoes ΔTC = 10 C°
10 cm steel ruler, B, undergoes ΔTC = 100 C°
Which will expand more?
B, will expand a factor of 10 greater A
Most of you already knew these results.
These results also lead to one conclusion:
ΔL = α L ΔT
Which states that the change of length of an object is dependant on
· Type of material
· Initial Length of material
· Change of temperature
Application of Thermal Expansion/Contraction / Question: What would happen if the coupling and the pipes were made of different materials and the entire new system became very hot or very cold?
Ans: Different materials have different coefficients of linear expansion, so if the coupling is a different material, the coupling would either crack (contract too much) or leak (expand too much)
This is the same principle as the bimetallic strip discussed in your book.
You are attempting to form the best junction between two pipes.
Use a coupling between pipes
· heat the coupling (torch)
· cool the ends of the pipes (ice bath or oil bath cooled with liquid nitrogen) / What happens to the coupling?
· it expands, including the hole in the middle
What happens to the pipes?
· they contract, become smaller
Slide the pipes into the coupling…let achieve room temp.
You now have a coupling as strong as the pipe itself.
Volume Thermal Expansion / Derivation:
à Remember Young’s Modulus…we now have another application
Young’s Modulus = Stress / Strain; where stress F/A and strain is ΔL/L
(Y) = F/A / ΔL/L
(Y) ΔL/L = F/A (= stress)
Stress = (Y) ΔL / L
; where ΔL = α L ΔT
Stress = (Y) α L ΔT / L
Stress = Y α ΔT
So if you know Young’s Modulus and the coef of linear expansion, you can calculate Stress.
First NOTE:
β equals 3 * α
Coef of Volume Expansion
= 3*(Coef of Linear Exp)
· Derivation below
And the formula follows similarly to linear expansion ΔL = α L ΔT
ΔV = β V ΔT / One of the notable exceptions to materials contracting as they get colder.
WATER!!! Water’s highest density is at 4 °C
This is very important for life, if you don’t see why…ask in CLASS!!!
Vo + DV = (l + Dl) (h + Dh) (w + Dw)
Vo + DV = (l + alDT) (h + ah DT) (w + aw DT)
Vo + DV = l*h*w (1 + aDT)3
Vo + DV = Vo (1 + 3aDT + 3(aDT)2 + (aDT)3)
DV/Vo = 3aDT + 3(aDT)2 + (aDT)3
We also know aDT <1 for most materials…so
DV/Vo = 3aDT
DV = Vo3aDT / Special Properties of water
Thermostat Demo: TH-A-DT
16.4 Heat and Mechanical Work
Units of heat / Heat is defined as the transfer of energy across the boundary of a system due to a temperature difference between the system and its surroundings.
calorie / the amount of energy transfer required to raise the temp of 1 gram of water from 14.5 °C to 15.5 °C
joule / The SI unit: 1 cal = 4.186 Joules
1 kcal = 1 Calorie = 4186 Joules
BTU / English unit: (Q required to raise 1 lb, 1 °F)
1 Btu = 1054 Joules
If work is done on a system, then the system will transfer energy across its boundary.
Work on system
The dentists drill causes your teeth to get hot…so cold water is sprayed on your teeth to cool down the teeth. The cold water is external to the system and its temperature raises when in contact with the hot tooth. / Work by system
If energy is added to a system, work may be done by the system.
Burn coal in a steam engine, and the steam engine is able to move the entire train.
16.5 Specific Heats
Heat Capacity, C : Q = C ΔT
C, the heat capacity is defined as the energy needed to raise the temperature of a sample by 1°C / Specific Heat: Q = m c ΔT c, the heat capacity of a sample per unit mass
Question: Which would require more energy to bring to boil if both are initially at room temperature?
A) A cup of water
B) A swimming pool full of water
Ans: I wouldn’t want to have to pay the energy bill required to raise a swimming pool full of water to its boiling point.
Conclusion: The greater the mass…the more energy required to bring to boiling point. / Question: Which would require more energy to rise from 20 °C to 50 °C?
A) A cup of water
B) A cup of alcohol
Ans: This one is harder…but I believe many know raising the temperature of alcohol requires less heat than water.
Conclusion: The material being heater makes a bit difference, so materials like water require much more energy to change its temperature compared to materials like alcohol and sand.
Question: Which would require more energy to bring to boil?
A) A cup of water at 20 °C
B) A cup of water at 90 °C
Ans: This one is easy…the one at 90 °C is almost at boil already, thus the energy input required to bring it to boil will way less than the cup at 20°C
Conclusion: The greater the ΔT…the greater amount of energy was required. / Question: Which would require more energy to bring to 20 °C?
C) A cup of ice at 0 °C
D) A cup of water at 0 °C
Ans: This one is easy…imagine adding 0°C water to your Coke or Pepsi to cool it down. 0°C ice requires much energy to bring it to 0°C water.
Conclusion: The change of state requires a large change of energy.
SI units are generally preferable, but I’m presenting this section in cgs units
Question: A large block of ice, 1000 g, is at -20 °C. How much energy is required to bring it to 100 °C steam?
Ans: v à vaporization f à fusion units of c à calories / (gram C°)
Q = cice m ΔT + m Lf + cwaterm ΔT + m Lv
Q = ½ (1000)(20) + 1000(80) + 1 (1000)(100) + 1000 (539)
Q = 10,000 cal + 80,000 cal + 100,000 cal + 539,000 cal
Q = 729,000 calories (1 Calorie = 1 kilocalorie)
Q = 729 Calories (4.186 J / Cal)
Q = 3052 Joules (a good exercise for you is to work the problem out using SI units)
16.6 Conduction, Convection, Radiation
Conduction
P = Q / t
P = kA ΔT/Δx
P = kA ΔT/Δx
P = A ΔT/(Δx/k)
P = A ΔT/(ΣRi) / Δx: The thicker the wall…more isolated
A: More area…
the more energy flows through the wall
ΔT: The greater the temperature difference…
the more energy flow through the wall
k: And different materials will have
different coefficients for heat flow /
R à ft2 °F hr/Btu
1 ft2 °F hr/Btu (0.305m/ft)2 (5°C/9°F)(3600s/hr)(1Btu/1054J)
1 ft2 °F hr/Btu = 0.1765 m2 °F sec / J
Standard 2x4 insulation is R-11 English units
In metric this would be R-2
Convection
Energy transferred by the movement
of a warm medium
Convection Currents in Air: TH-B-CC / Radiation
Stefan’s Law: P = σAeT4
σ = 5.669 x 10-8 W/m2K4,
e is emissivity (0 to 1)
Ideal absorber, e = 1 (Black Body)
Ideal reflector, e = 0
Demo: Light the Match: TH-B-LM
Crooke’s Radiometer Demo: TH-D-CR
Boddeker's Ch 16 Temperature and Heat (PHY122)